티스토리 뷰
문제1.
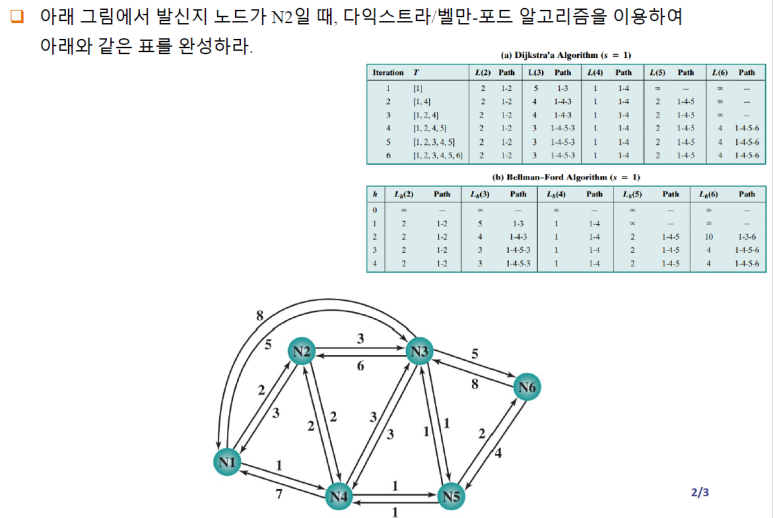
답.
1) 다익스트라 알고리즘
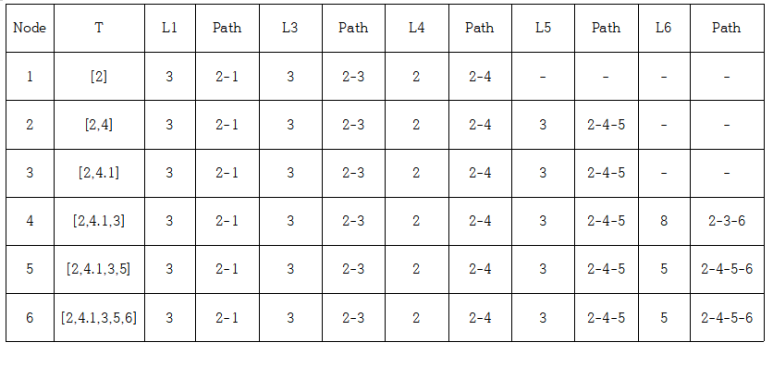
2) 벨만 포드 알고리즘
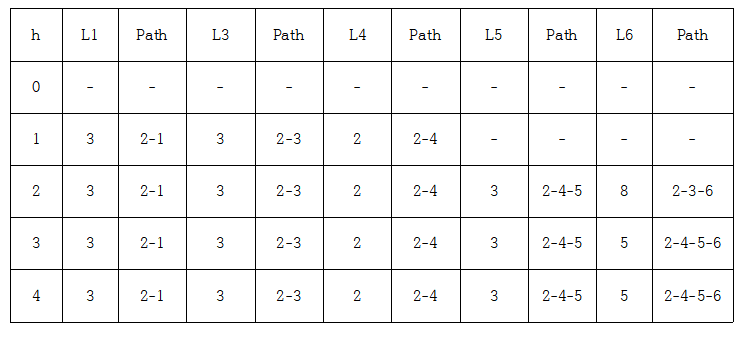
문제2.
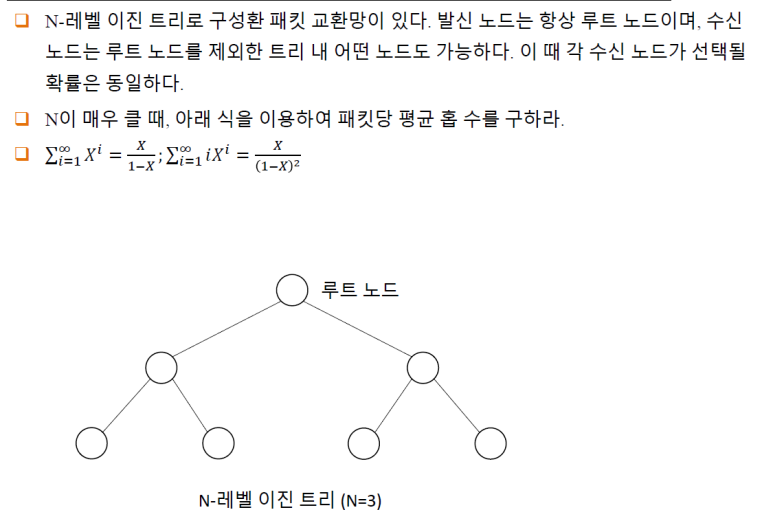
답.
먼저 N 레벨 이진트리의 특징을 알아야 한다.
1. N 레벨 이진트리의 N 레벨에 있는 노드 수는 2^(N-1) 개 이다.
ex. 4 레벨 이진트리의 4레벨에 있는 노드의 개수는 2^(4-1) = 8 개이다.
2. N 레벨 이진트리의 N 레벨을 제외한 모든 노드의 수는 2^(N-1) - 1 개 이다.
ex. 4 레벨 이진트리의 1~N-1레벨까지의 모든 노드의 수는 2^(4-1) -1 = 7 개이다.
3. 루트에서 N 레벨 까지 가는데 거쳐가는 경로는 N-1이다.
ex. 4레벨 이진트리에서 4레벨 노드까지 가는데 거쳐가는 가지(홉 수)는 4-1 = 3가지이다.
그럼 N레벨에 있는 노드를 기준으로 보자.
N 레벨에 있는 노드의 수는 2의 n-1승 개이고, 나머지 모든 노드 수의 합은 그것보다 1개 적다. ( 1,2번 특징 )
n이 무한히 크다고 문제에서 가정했으므로, (N레벨에 있는 노드 수 ) = (나머지 노드 수 ) 라고 볼 수 있다.
( N이 무한히 크면 1개차이는 무시할 수 있으므로 )
따라서 N레벨에 있는 노드가 선택될 확률은 1/2 이다. N레벨 까지가는 데 거치는 홉 수는 N-1 개이다.
정리하면 N레벨에 있는 노드가 선택되서 그곳까지 가는 홉수 = (1/2)*(N-1) 이다.
N-1레벨에 있는 노드가 선택될 확률은 다시 절반 이므로 (1/2)^2 이고 홉수는 (N-2) 가 된다.
이를 루트노드까지 전부 더하면
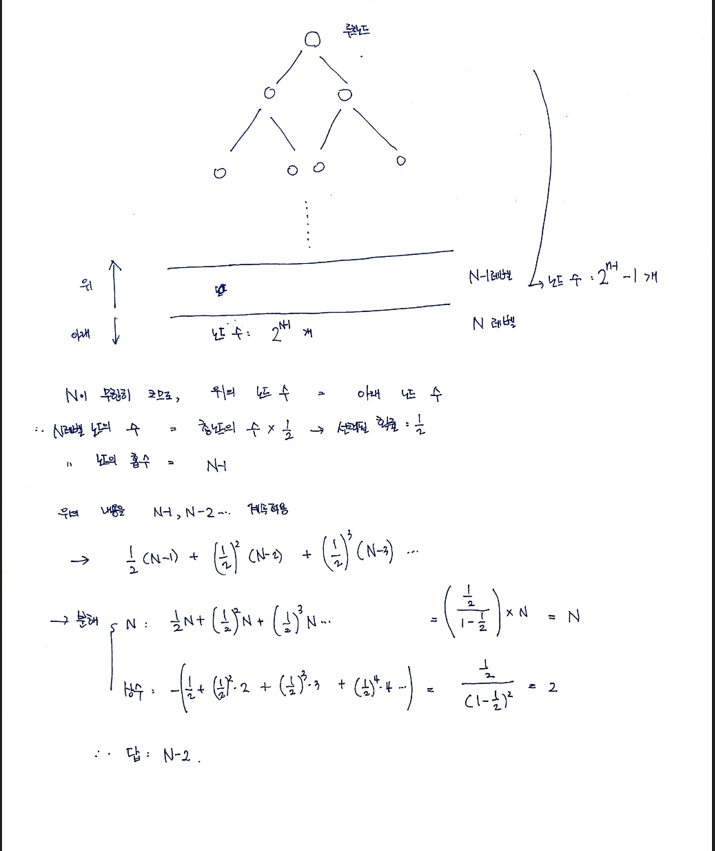
(1/2)*(N-1) + (1/2)^2*(N-2) ......이다. 여기서 N은 N끼리 묶고, 상수는 상수끼리 묶어서 문제의 공식을 적용하면 답은 N-2가 된다.
이해를 돕기 위해 아래에 풀이과정을 첨부했다.
'전공 > 컴퓨터 네트워크' 카테고리의 다른 글
| 11. 혼잡제어 연습문제 (0) | 2023.01.08 |
|---|---|
| 10. 혼잡제어 ( Congestion control ) (0) | 2023.01.08 |
| 8. Routing ( 경로 배정 ) (0) | 2023.01.08 |
| 7. ATM 연습문제 (1) | 2023.01.08 |
| 6. 비동기 전송 모드 ( ATM ) (1) | 2023.01.08 |
- Total
- Today
- Yesterday
- Instnat-ngp
- 아키텍처 설계
- 인터넷프로토콜
- 회선교환
- 클래스 모델링
- Instant-NGP
- 인터네트워크
- 전송계층프로토콜
- 설계 원리
- 디자인 패턴
- Extension to Regular Expression
- lan
- CUDA VISUAL STUDIO 2022 지원
- ngp 오류
- 컴퓨터네트워크
- Regular Expression
- ngp 실행
- 백준 2437
- Transition Function
- 소프트웨어공학
- 소프트웨어 공학
- Compiler
- NGP-ERROR
- 비동기전송모드
- Proper CFL
- Ambiguity
- 혼잡제어
- ATM
- 셀룰러네트워크
- 컴파일러
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
